昨天在朋友圈发了一个生日悖论的问题,想看看大家的计算结果。
问题是这样的:
在一个23人以上的班级中,有两个人生日是同一天的概率是多少?
More...
答案五花八门:
- 概率太低,没办法算,这是前世修来的福分,要好好珍惜
- 365分之一的平方
- 365的23次方
- 不到1%?
- 现在双胞胎概率比这个大
- ……
当然,也有人以自己的实例验证
- 我就和我同学一样
- 我们班里就有一对,好神奇
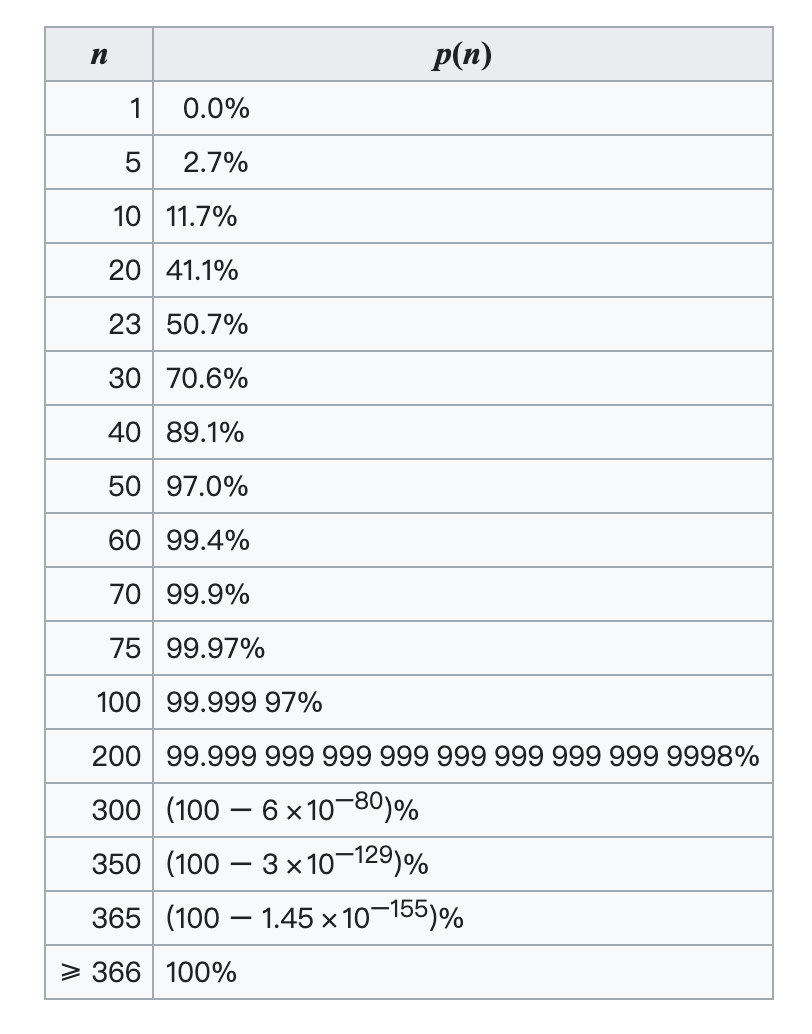
今天,我公布了答案:概率为50.7%,
也就是说,在任何有23人以上的班级中,有两个人生日是同一天的概率在一半以上。
并没有很多人想象的那么低。
很多人吓了一跳。
事实上,如果班里有60个人,那么概率有99%。
假如班里有366人(考虑闰年),那么概率是100%。
不谈数学计算的能力问题,从直觉反应来说,很多人认为这个比例很小,
问题的关键在于,很多人把这个匹配成功概率加在自己头上,而忽视了别人成功匹配的概率。
现实生活中,假如你要遇到另一个人,和你同一天生日,概率基本上是0.00273973,即1/365(不考虑闰年)
假如你是闰年闰月闰日出生的,那么你要找到同一天生日的另一个人的概率,那就是极低了。
